4.6. n-tās pakāpes saknes jēdziens un darbības ar saknēm
Par n-tās pakāpes sakni no skaitļa a sauc tādu skaitli b, kuram bn=a. Tātad
.
Ja n ir pāra skaitlis, tad 
eksistē tikai tad, ja a≥0 un b≥0. Piemērs.
Ja n ir nepāra skaitlis, tad eksistē visām a vērtībām. Piemērs.
| Sakņu īpašības |
| Īpašība |
Piemērs |
Ja a>0 un n,m,k N,  |
 |
|
Ja a>0, n, m, kN un k ir n un m kopīgais dalītājs
|
 |
Ja a≥0 un b≥0, tad  |
 |
Ja a≥0 un b>0, tad  |
 |
Ja a>0, n, m
N,  |
 |
Ja a≥0, n, m
N,  |
 |
| Ja saknes rādītājs ir nepāra skaitlis un zemsaknes skaitlis negatīvs, tad mīnus zīmi var iznest pirms saknes simbola. |
 |
|
Lai pozitīvu reizinātāju b ienestu zem, tad b jākāpina n-tajā pakāpē; 
Ja b ir negatīvs, tad mīnus zīme paliek pirms saknes.
|
|
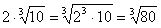